In the far 2007 year I developed an appearance of my own logotype. Now I gonna completely discribe it and make a model in 3DS Max program. Since I don’t have any vector graphics drawing software I gonna use the same program for 2D vector graphics.

I defined logotype as two hemitoruses with a torus inside. Let’s start with two circle arcs.

\[R = 10\] \[C_1(0, 0)\] \[C_2(-R, -R)\]

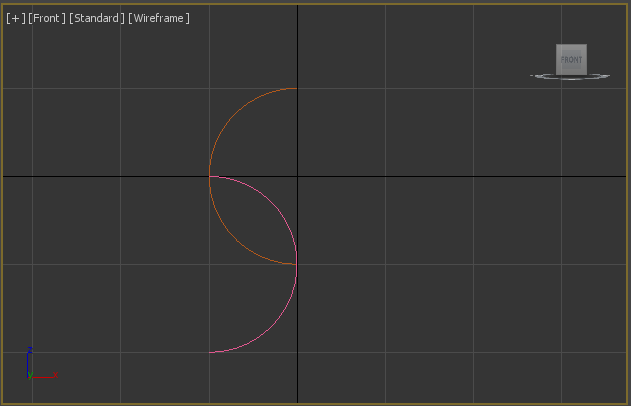
The classic view of logotype is with center of second arc $C_2$ lying on the first arc.

\[C_2(x_0, z_0)\]

The first arc has equation:

\[x = -\sqrt{R^2-z^2} \tag{1}\label{1}\]

Putting coordinates of point $C_2$ into equation $\eqref{1}$ we get following equation:

\[x_0 = -\sqrt{R^2-z_0^2} \tag{2}\label{2}\]

Also there is a point $P_1$ on the same vertical line that lyes on the first arc:

\[P_1(x_0, z_0+R)\]

The point opposite to $P_1$ is known, let’s call it $P_2$:

\[P_2(0,-R)\]

Putting coordinates of point $P_1$ into equation $\eqref{1}$ we get following equation:

\[x_0 = -\sqrt{R^2-(z_0+R)^2} \tag{3}\label{3}\]

To find $x_0$ and $z_0$ we should solve the system of two equations:

\[\left\{ \begin{array}{ll} x_0 = -\sqrt{R^2-z_0^2} \\ x_0 = -\sqrt{R^2-(z_0+R)^2} \end{array} \right. \tag{4}\label{4}\]

Solved system has the following view:

\[\left\{ \begin{array}{ll} x_0 = -R\frac{\sqrt{3}}{2} \\ z_0 = -R\frac{1}{2} \end{array} \right.\]

So

\[C_2(-R\frac{\sqrt{3}}{2},-R\frac{1}{2})\]

Now we need to compute length of inner torus. It’ perpendicular to the line $P_1P_2$. Middle point of line $P_1P_2$ is simple:

\[\left\{ \begin{array}{ll} P_{cx} = (P_{1x} + P_{2x})/2 \\ P_{cy} = (P_{1y} + P_{2y})/2 \end{array} \right.\] \[P_c(\frac{x_0}{2},\frac{z_0}{2})\]

Ok, now I apologize that line $C_2O$ is what we are looking for. Lets prove it:

\[\overrightarrow{C_2O}=(x_0,z_0)\] \[\overrightarrow{P_2P_1}=(x_0,z_0+2R)\] \[\overrightarrow{C_2O}\cdot\overrightarrow{P_2P_1} = x_0^2 + z_0(z_0+2R)\] \[\overrightarrow{C_2O}\cdot\overrightarrow{P_2P_1} = R^2\frac{3}{4} + (-R\frac{1}{2})(-R\frac{1}{2}+2R)\] \[\overrightarrow{C_2O}\cdot\overrightarrow{P_2P_1} = R^2\frac{3}{4} + R^2\frac{1}{4} - R^2\] \[\overrightarrow{C_2O}\cdot\overrightarrow{P_2P_1} = 0\]

So the length of the inner torus should be:

\[|\overrightarrow{C_2O}| = \sqrt{R^2\frac{3}{4}+R^2\frac{1}{4}} = R\]

And let’s compute the angle of inner torus inclination:

\[\alpha = atan(\frac{x_0}{z_0}) = atan(\sqrt{3}) = 60^\circ\]

The final view of arcs will be following:

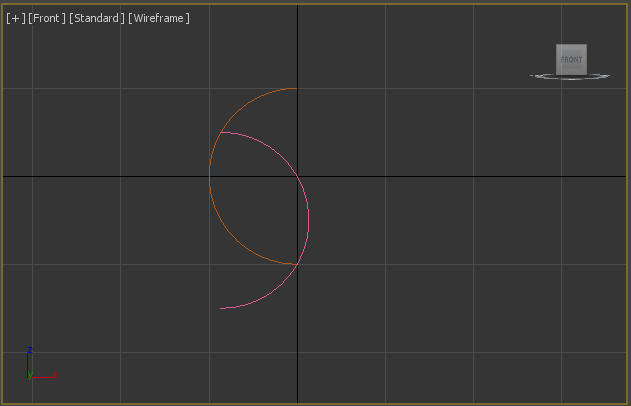
The original model consists of two toruses and one figure of rotation. I’ve defined the torus radiuses ratio $R1/R2$ as 10. The “eye” is a figure of rotation, based on arc.

Lets model a two toruses models (nice pun). We can simply use one torus and truncate it.

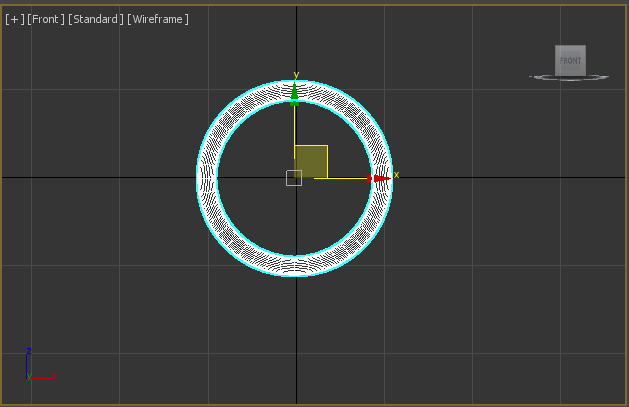
Detach part of the torus:

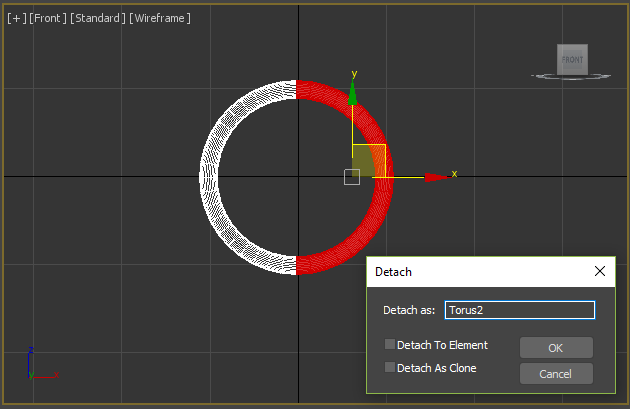
Then move it to a proper position:

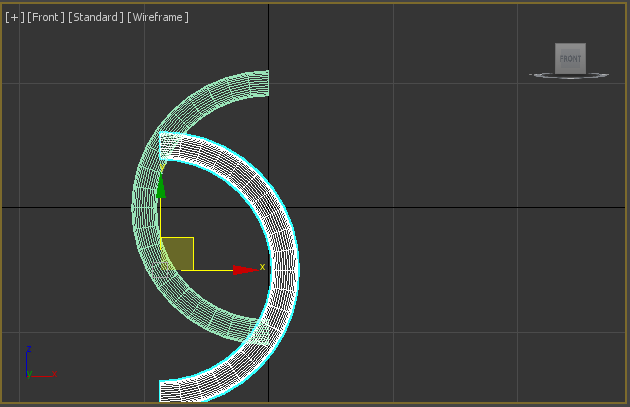
Do the same with sphere and close the ends:

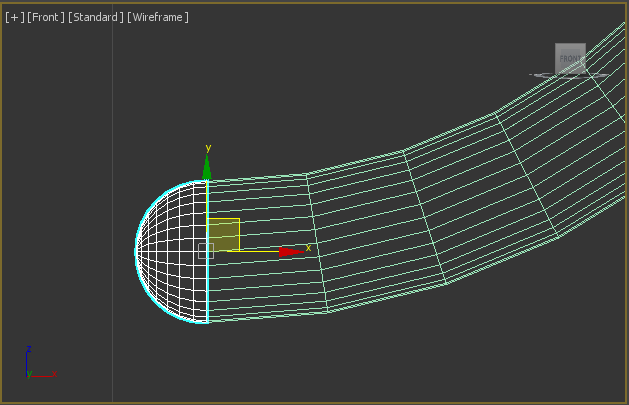
Now we can make the “eye”. It’s defined by arc with length equal to $R$. And it should be two times wider than original torus. Lets call it $H$:

\[\left\{ \begin{array}{ll} R_e = R_e \cdot cos(\alpha) + H \\ R_e \cdot sin(\alpha) = L/2 \\ H = \frac{2}{10}R \\ L = R-\frac{2}{10}R \end{array} \right.\] \[\left\{ \begin{array}{ll} R_e = \frac{R}{2} \\ \alpha = 2 \cdot atan(\frac{1}{2}) \end{array} \right.\]

Now we’re able to create a inner torus:

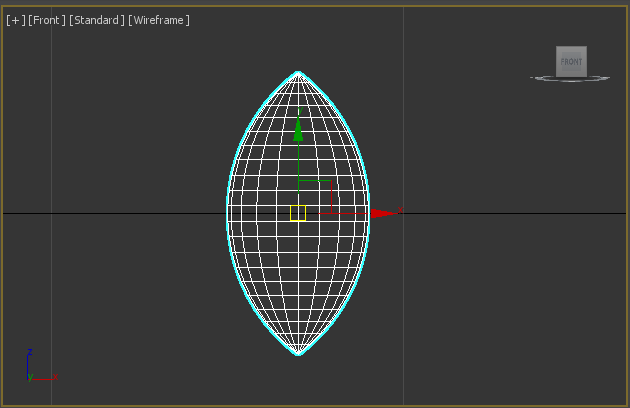
After all object is placed and attached together:

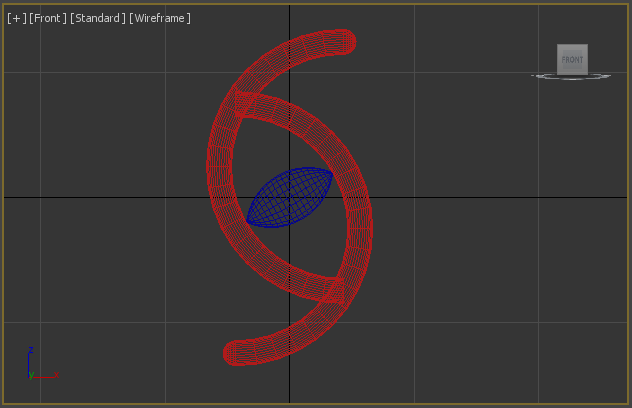
Now I can use this model for rendering in my framework:

That’s all!